Gravity potential values at optical clock comparison sites

Introduction

Due to the high performance of atomic clocks and time transfer techniques, the definition of timescales and clock comparison procedures must be handled within the framework of general relativity. This leads to the relativistic redshift correction that has to be applied for each atomic clock in order to refer to a worldwide uniform timescale, i.e. Terrestrial Time (TT). Terrestrial time is a coordinate timescale that may be associated with a virtual clock located on the (zero) reference potential surface (geoid), and both TAI (International Atomic Time) and UTC (Coordinated Universal Time) can be considered as realizations of TT.

Considering the usual case of two earthbound clocks at rest, the relativistic redshift effect is directly proportional to the corresponding gravity (gravitational plus centrifugal) potential difference between both sites, where one part in 1018 clock performance corresponds to about 0.1 m2/s2 in terms of the gravity potential, which is equivalent to 0.01 m in height. Hence, geodetic knowledge of heights and the Earth's gravity potential can be used to predict frequency shifts between local and remote (optical) clocks, and vice versa, the clocks can be used to determine gravity potential differences, the latter technique being also denoted as 'chronometric levelling' or 'relativistic geodesy'. In this context, absolute gravity potential values with respect to a conventional zero value are needed for contributions to international timescales, while potential differences suffice for local and remote clock comparisons. Furthermore, following standard geodetic practice, the gravity potential is considered as a static quantity, and hence it is assumed that time-variable components of the gravity potential (the largest being tidal effects) are taken into account by corresponding reductions (see more) or have been averaged out by sufficiently long observation time spans.

Methods

The gravity potential is closely interrelated with the question of heights and the geoid, where the geoid is defined as a selected level surface with constant gravity potential, conceptionally chosen to approximate the mean ocean surface. The geoid serves as the reference surface for the orthometric heights, which can be converted into corresponding gravity potential differences (geopotential numbers) by a mean gravity value. Accordingly, the quasigeoid serves as the height reference surface for the normal heights, with the conversion to gravity potential differences relying on a mean normal gravity value.

In the ITOC project, two different approaches are used to compute the gravity potential values at all relevant clock sites. The first most direct and accurate geodetic approach over short distances is the geometric levelling technique (plus gravity observations), which initially delivers only height or potential differences with respect to a conventional datum point, typically attached to a tide gauge and mean sea level. The geometric levelling techniques determines height differences by horizontal lines of sight; it can achieve millimetre accuracy or better, but as it is a differential technique (see Fig 1), it is susceptible to systematic errors, which may accumulate to the level of decimetres over 1,000 km distance. A further complication with geometric levelling in different countries is that the results are usually based on different tide gauges, and due to the existence of the dynamic ocean topography, each height reference system has its own reference level surface, leading to inconsistencies of more than 0.5 m between different national height reference systems across Europe (see Fig 2). This has been taken into account by transforming the national heights, provided by the respective metrological institutes (NMIs), into the unified European Vertical Reference System (EVRS) with the realization EVRF2007.

The second approach is based on GNSS positions and the results from gravity field modelling (geoid, quasigeoid), and it is therefore denoted as the GNSS/geoid approach. In principle, the difference between the GNSS ellipsoidal height and the geoid height gives the orthometric height and thus the geopotential number, and this works accordingly with the quasigeoid and normal height. High precision ellipsoidal coordinates for selected sites near the clock laboratories have been provided again by the respective NMIs (for an example see Fig 3). All GNSS coordinates have been transformed to a unified reference frame and epoch. The advantage of the GNSS/geoid approach is that it can deliver the absolute gravity potential values, and thus it can also be used to derive the numerical value of the zero potential associated with geometric levelling. The accuracy of the heights and potential values based on the GNSS/geoid approach depends critically on the accuracy of the input GNSS and gravity field data, leading in the best case (sufficient terrestrial gravity field data around sites of interest, state-of-the-art global satellite gravity field models and GNSS data) to an accuracy of about 2-3 centimetres in terms of height. However, regarding the determination of potential differences over longer distances of 1,000 km or more, the levelling and GNSS/geoid approaches become at least competitive and especially with further improved global satellite gravity field models, the GNSS/geoid approach should be beneficial.

Results

Gravity potential values based on the geometric levelling and the GNSS/geoid approach have been computed for all relevant clock sites. They are based on the EVRF2007 levelling datum, as well as the European Gravimetric Quasigeoid 2015 (EGG2015, see Fig 4), which also includes the additional gravity observations carried out around the involved NMIs within the framework of the ITOC project, as well as the state-of-the-art GOCE-based geopotential model GOCO05S.

The gravity potential values and the associated heights based on the GNSS/geoid approach and the levelling approach have been compared, showing inconsistencies between both procedures at the decimetre level across Europe. Hence, the more or less direct observation of gravity potential differences through optical clock comparisons with targeted fractional accuracies of 10^-18 (corresponding to 1 centimetre in height) is eagerly awaited to overcome some of the limitations inherent in the classical geodetic techniques, especially to solve the geodetic height determination problem over large distances.

Fig 1:  Geometric levelling at Bushy House, National Physical Laboratory (NPL), UK

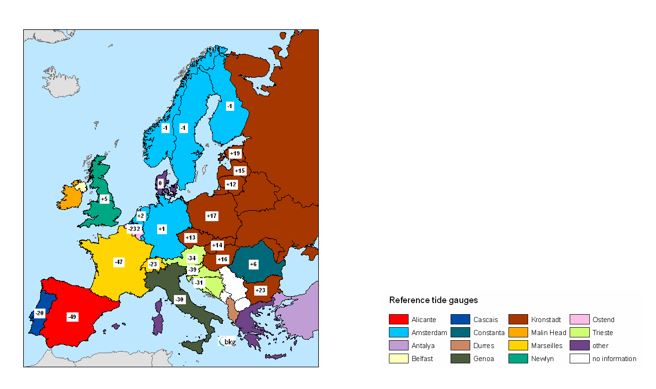
Fig 2:  Differences between national height reference systems (based on different tide gauges) and EVRF2007 in centimetres (see https://www.bkg.bund.de/DE/Ueber-das-BKG/Geodaesie/Integrierter-Raumbezug/Hoehe-Europa/hoehe-europa.html

Fig 3:  GNSS antennas at Physikalisch-Technische Bundesanstalt (PTB)

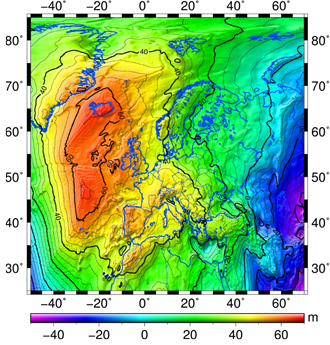
Fig 4:  European gravimetric quasigeoid model EGG2015

The research within this EURAMET joint research project receives funding from the European Community's Seventh Framework Programme, ERA-NET Plus, under Grant Agreement No. 217257.